Modélisation linéaire étendue

Introduction aux caractéristiques polynomiales

Les modèles linéaires entraînés sur des fonctions non linéaires de données conservent généralement les performances rapides des méthodes linéaires. Cela leur permet également de s'adapter à un éventail de données beaucoup plus large. C'est la raison pour laquelle les modèles linéaires formés sur des fonctions non linéaires sont utilisés dans l'apprentissage automatique.

Par exemple, une régression linéaire simple peut être étendue en construisant des caractéristiques polynomiales à partir des coefficients.

Mathématiquement, supposons que nous ayons un modèle de régression linéaire standard, alors, pour des données bidimensionnelles, il ressemblerait à ceci :

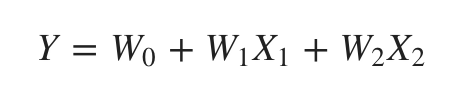
Maintenant, nous pouvons combiner les caractéristiques dans des polynômes du second ordre et notre modèle ressemblera à ce qui suit :

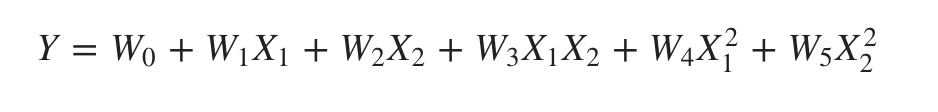
Le modèle ci-dessus est toujours un modèle linéaire. Ici, nous avons vu que la régression polynomiale résultante est dans la même classe de modèles linéaires et peut être résolue de manière similaire.

Pour ce faire, scikit-learn fournit un module nommé PolynomialFeatures. Ce module transforme une matrice de données d'entrée en une nouvelle matrice de données de degré donné.

Paramètres

La liste suivante présente les paramètres utilisés par le module PolynomialFeatures :

• degree - nombre entier, par défaut = 2. Il représente le degré des caractéristiques polynomiales.
• interaction_only - booléen, par défaut = false. Par défaut, il est faux mais s'il est défini comme vrai, les caractéristiques qui sont des produits de caractéristiques d'entrée distinctes au degré le plus élevé, sont produites. Ces caractéristiques sont appelées caractéristiques d'interaction.
• include_bias - Booléen, par défaut = true. Il inclut une colonne de biais, c'est-à-dire la caractéristique dans laquelle toutes les puissances des polynômes sont nulles.
• order - str dans {'C', 'F'}, par défaut = 'C'. Ce paramètre représente l'ordre du tableau de sortie dans le cas dense. L'ordre 'F' est plus rapide à calculer, mais d'un autre côté, il peut ralentir les estimateurs suivants.

Attributs

Le tableau suivant présente les attributs utilisés par le module PolynomialFeatures :

• powers_ - tableau, forme (n_output_features, n_input_features). Il montre que powers_ [i,j] est l'exposant de la jème entrée dans la ème sortie.
• n_input_features_ - int. Comme son nom l'indique, elle donne le nombre total de caractéristiques d'entrée.
• n_output_features_ - int. Comme son nom l'indique, il donne le nombre total de caractéristiques polynomiales en sortie.