Modèle linéaire : Elastic-Net

L'Elastic-Net est une méthode de régression régularisée qui combine linéairement les deux pénalités, c'est-à-dire L1 et L2, des méthodes de régression Lasso et Ridge. Elle est utile lorsqu'il existe de multiples caractéristiques corrélées. La différence entre Lasso et Elastic-Net réside dans le fait que Lasso est susceptible de choisir l'une de ces caractéristiques au hasard alors que Elastic-Net est susceptible de choisir les deux en même temps.

Sklearn fournit un modèle linéaire nommé ElasticNet qui est entraîné avec les deux normes L1 et L2 pour la régularisation des coefficients. L'avantage d'une telle combinaison est qu'elle permet d'apprendre un modèle clairsemé où peu de poids sont non nuls comme la méthode de régularisation Lasso, tout en conservant les propriétés de régularisation de la méthode de régularisation Ridge.

La fonction objective à minimiser est la suivante :

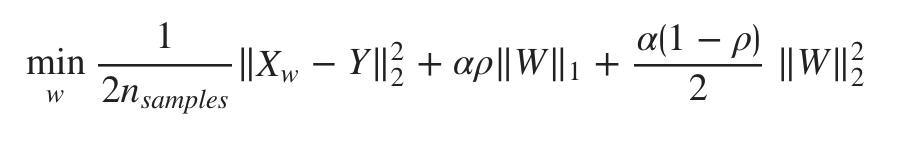
Paramètres

La liste suivante présente les paramètres utilisés par le module ElasticNet :

• alpha - flottant, facultatif, par défaut = 1,0. Alpha, la constante qui multiplie le terme L1/L2, est le paramètre d'accord qui décide dans quelle mesure nous voulons pénaliser le modèle. La valeur par défaut est 1.0.
• l1_ratio - float. Il s'agit du paramètre de mélange ElasticNet. Sa plage est 0 < = l1_ratio < = 1. Si l1_ratio = 1, la pénalité serait une pénalité L1. Si l1_ratio = 0, la pénalité serait une pénalité L2. Si la valeur de l1_ratio est comprise entre 0 et 1, la pénalité serait la combinaison de L1 et L2.
• fit_intercept - Booléen, facultatif. Par défaut=True. Ce paramètre indique qu'une constante (biais ou intercept) doit être ajoutée à la fonction de décision. Aucun intercept ne sera utilisé dans le calcul, s'il est défini à false.
• tol - flottant, facultatif. Ce paramètre représente la tolérance pour l'optimisation. La valeur tol et les mises à jour seront comparées et si les mises à jour trouvées sont inférieures à tol, l'optimisation vérifie l'optimalité du double écart et continue jusqu'à ce qu'il soit inférieur à tol.
• normalise - Booléen, facultatif, par défaut = False. Si ce paramètre est défini sur True, le régresseur X sera normalisé avant la régression. La normalisation sera effectuée en soustrayant la moyenne et en la divisant par la norme L2. Si fit_intercept = False, ce paramètre sera ignoré.
• precompute - True|False|array-like, default=False. Avec ce paramètre, nous pouvons décider d'utiliser une matrice de Gram précalculée pour accélérer le calcul ou non. Pour préserver la sparsité, il sera toujours vrai pour une entrée peu dense.
• copy_X - Booléen, facultatif, par défaut = True. Par défaut, il est vrai, ce qui signifie que X sera copié. Mais s'il est défini à false, X peut être écrasé.
• max_iter - int, optionnel. Comme son nom l'indique, il représente le nombre maximum d'itérations prises pour les solveurs de gradient conjugué.
• warm_start - bool, optional, default = false. Avec ce paramètre réglé sur True, nous pouvons réutiliser la solution de l'appel précédent à fit comme initialisation. Si nous choisissons la valeur par défaut, c'est-à-dire false, cela effacera la solution précédente.
• random_state - int, RandomState instance ou None, facultatif, par défaut = none. Ce paramètre représente la graine du nombre pseudo-aléatoire généré qui est utilisé lors du brassage des données. Les options suivantes sont disponibles :
  • int - Dans ce cas, random_state est la graine utilisée par le générateur de nombres aléatoires.
  • RandomState instance - Dans ce cas, random_state est le générateur de nombres aléatoires.
  • None - Dans ce cas, le générateur de nombres aléatoires est l'instance RandonState utilisée par np.random.
• selection - str, default='cyclic' (sélection)
  • Cyclic - La valeur par défaut est cyclique, ce qui signifie que les caractéristiques seront bouclées séquentiellement par défaut.
  • Random - Si nous définissons la sélection comme aléatoire, un coefficient aléatoire sera mis à jour à chaque itération.

Attributs

La liste suivante présente les attributs utilisés par le module ElasticNet :

• coef_ - tableau, forme (n_tâches, n_caractéristiques). Cet attribut fournit les vecteurs de poids.
• Intercept_ - tableau, forme (n_tasks). Il représente le terme indépendant dans la fonction de décision.
• n_iter_ - int. Il donne le nombre d'itérations effectuées par le solveur de descente de coordonnées pour atteindre la tolérance spécifiée.

Exemple d'implémentation